Problems with ChatGPT

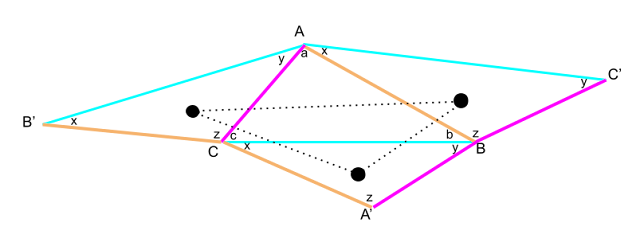
I've been an occasional user of ChatGPT for about a year. It occasionally is truly impressive but today I had an interaction with it that, in many ways was both weirdly human and stubbornly wrong. I had been investigating a geometrical question:

What is the condition that the midpoints of a quadrilateral form a square?

I began by telling ChatGPT that I knew that the midpoints of a quadrilateral always formed a parallelogram. It agreed and gave me the proof that requires two applications of the midpoint theorem. Then came this dialogue

Me: For what type of quadrilateral is this parallelogram a square?

ChatGPT: The parallelogram formed by the midpoints of the sides of a quadrilateral is a square if and only if the original quadrilateral is a rectangle.

This was followed by several lines of proof which included the claim that the diagonals of a rectangle intersect at right angles. ChatGPT's claim is false and I pointed this out saying that it could not be true for long thin rectangles. So then....

ChatGPT: You are correct, and I apologize for the confusion. Let's revisit the conditions under which the parallelogram formed by the midpoints of a quadrilateral's sides is a square.

Then came...

ChatGPT: For the parallelogram formed by the midpoints of a quadrilateral's sides to be a square, the original quadrilateral must be an isosceles trapezoid.

More dialogue in which I again refuted this claim with long thin isosceles trapezoids to which I got:

ChatGPT: I apologize for the confusion earlier. You are right; neither rectangles nor isosceles trapezoids in general guarantee that the midpoints of their sides will form a square under all circumstances. Let's clarify the exact condition needed for the parallelogram formed by the midpoints to be a square.

ChatGPT: For the parallelogram formed by the midpoints of a quadrilateral to be a square, the quadrilateral must be a rhombus.

Another refutation by me and then ChatGPT returned to its original declaration that the quadrilateral had to be a rectangle. And finally...

ChatGPT: I appreciate your patience and the opportunity to clarify this correctly.

At that point I could not get much change in ChatGPT's replies. Its geometrical reasoning was superficially plausible in that it set out its arguments in a logical progression of steps. I have to confess I would have been hugely impressed had it got its logic correct. But the weirdly human aspect of it was its insistence, despite all the evidence, that it was right all along.

And I guess the moral of this interaction is that, despite its answers being couched in the most plausible of clothes, it was entirely wrong. And so, be careful, perhaps it is wrong lots of times.

Napoleon's theorem

I'm an avid follower of Mathologer videos and his latest on the Petr-Douglas-Neumann theorem was well up to his high standards. I hope to write another post on that video but today I am commenting on a special case - Napoleon's theorem - that many others have also discussed.

Seemingly there is no definite connection with Napoleon Bonaparte, or any other Napoleon, but the theorem does seem to have made its debut in the mathematical literature in the early part of the nineteenth century. So, given that Napoleon had many renowned mathematical friends and was keenly interested in science, it is possible that a connection may exist.

In its basic form Napoleon's theorem is:

Let ABC be any triangle. Then the centroids of the 3 equilateral triangles with bases AB, BC, CA erected on the outside of triangle ABC form an equilateral triangle.

There are several proofs and generalisations. The proof that I give below is similar to the one here but handles one of the known generalisations of the theorem.

First some terminology. 

We shall deem two triangles to be similar if one can be transformed into the other by a translation, scaling factor, and rotation. In particular this means that the set of interior angles of one triangle is the same as the other and these angles occur in the same order around their triangle. The second condition is not always part of the definition of similarity.

If we think of our similar triangles as lying in the plane where every point is a complex number then we have the following necessary and sufficient condition that the triangle with vertices (z₁, z₂, z₃) is similar to the triangle with vertices (w₁, w₂, w₃):

This (elementary) result is proved here which refers to G. H. Hardy's classic textbook. It follows immediately from properties of determinants that triangle z₁z₂z₃ is  similar to every triangle pz₁+qw₁,pz₂+qw₂,pz₃+qw₃, with p and q not both zero. This extends to three (the case we shall use) or more similar triangles: if we have three similar triangles then any weighted sum of them will be a triangle similar to the summands.

Now we are ready to present the generalisation of Napoleon's theorem.  We begin with an arbitrary triangle and erect, on each side, 3 similar  triangles as shown below:

The diagram shows the three similar triangles in question as AC'B, CBA', B'AC. The angles and colours are intended to indicate the similarity correspondences. The three black dots are the centroids of the similar triangles.

So we have AC'B ~ CBA' ~ B'AC.

Now we take a weighted sum of these three triangles with weights 1/3, 1/3, 1/3. This gives a triangle with vertices (A+C+B')/3, (C'+B+A)/3, (B+A'+C)/3. From the discussion above this triangle is similar to the three original triangles. But these vertices are also the centroids of the original similar triangles.

I believe this proof is a lot more concise than most of the others and, of course, it proves something more general. One of the interesting aspects of the proof is that the technique of coordinatising the plane was not discovered until Descartes; so the proof could not have been discovered by the classical geometers.

In the case that the 3 similar triangles are equilateral this gives Napoleon's theorem. But different choices for the weights other than 1/3, 1/3, 1/3 give other interesting results. For example with weights 1/2, 0, 1/2 we get a triangle where the vertices are the midpoints of C'B, BA', AC (the midpoints of the green edges); this too is similar to the original similar triangles.

In the case that the triangles are equilateral we get another equilateral triangle.