Tuesday, 31 December 2024
A remarkable year
Sunday, 25 August 2024
Polygonal musing
Recently I was very taken by a Mathologer video on polygons. Clearly I was not the only one because it already has been viewed about 150,00 times. The video is about the Petr-Douglas-Neumann theorem and I have already been inspired to blog about the special case of triangles (Napoleon's theorem). Today I would like to give a bird's eye view of the theorem and its proof. Then I shall give some thoughts to do with polygons in general which have been suggested by the proof of the general theorem.
First, for completeness, let me briefly describe what the theorem says. It begins with an arbitrary n-gon and then transforms it into a succession of n-2 further n-gons. A typical step Sr takes the current polygon and erects isosceles triangles on each of its sides; each side is the base of an isosceles triangle, and the apex angle of the triangle is an angle chosen from the set A = {360r/n | r =1,...,n-1}. The next polygon is this sequence of triangle apexes (or ears as Mathologer calls them). These ears appear on the left of each side (travelling clockwise) but, when the apex angle is greater than 180, they are on the right of the edge. The theorem's conclusion is that, after a series of n-2 steps with distinct angles chosen from the set A, the final n-gon is regular.
I encourage you to watch the video if only for the compelling animations used to describe the sequence of polygons. You will see (as Mathologer observes) that the polygons become increasing regular looking (whatever that means - but see below!).
Mathologer explains that one must consider every polygon to be an ordered sequence of complex numbers (each complex number representing a point in the Argand diagram). Then there is a special set of n regular polygons Pr (r = 0, 1, 2,..., n-1) where the corresponding sequences of complex numbers has the form (1,wr,w2r,...,w(n-1)r) with w representing a complex nth root of unity. He notes that this set polygons is a set of linearly independent vectors in n-dimensional complex space.
Therefore the initial arbitrary polygon is a linear combination of the n special polygons.
The next observation (which Mathologer only sketches) is that each step Sr which transforms a set of points (considered as a vector) into another set of points is actually a linear transformation. This fact is left to the reader to verify but, actually, it is not very difficult: each component in the new set of points depends on two of the points in the original vector and, when one calculates what it is from the geometrical construction, it turns out to be a linear formula.
The actual linear transformation effected by Sr is a bit too complicated to express in the typography provided by this blogging software (do I hear echoes of Fermat's last theorem?). You can find it in the video by John Harnad; and, in fact, two crucial facts flow from this formula. The first is that, if Sr is applied to Pr, the result is zero. The second is that, if Sr is applied to Pt with r≠t, the result is a polygon similar to Pt.
The proof of the theorem is now clear. The starting polygon is a linear combination of the n special polygons Pr. When a step of the form Sr is applied, the coefficient of Pr in this linear combination is reduced to zero. Once n-2 steps have been applied only one summand in the linear combination is non-zero; but that is a regular polygon.
We can now quantify the meaning of "becoming increasingly regular looking". At the beginning there is nothing special about the chosen polygon: it can be as irregular as possible. But after one step it is restricted: it is now in the linear span of n-1 of the Pr. And after each successive step it is in the linear span of fewer and fewer of the Pr, until at the end it is in the linear span of just one Pr.
Another way of putting this is that there is a hierarchy of increasingly restrictive types of polygon, depending on the increasingly restrictive linear spaces that the polygon belongs to. It is interesting to compare this with the conditions that classical types of polygons satisfy and this is particularly the case for triangles and quadrilaterals.
For example, what about equilateral triangles? Not all equilateral triangles are the same of course. They differ in their position in the plane, their size, and their rotation and so we have to think about the class of all such triangles, and we should also allow the triangle with all side lengths equal to zero. But that is not all! It is crucial whether we allow two equilateral triangles which are reflections of one another to be the same. Depending on whether we allow this or not we shall have one or two classes of equilateral triangles.
In the first case the set of all equilateral triangles is not a linear space (indeed it spans the entire set of triangles). In the second case it is a two-dimensional subspace (spanned, for example, by the one point triangle (0,0,0) and either the triangle (1,w,w2) or the triangle (1,w2,w) where w is a cube root of 1).
This suggests that when we consider other classical polygons it will be more interesting if we consider classes closed under displacement, inflation, and rotation but not reflection. We'll do that from now on.
What about the set of all triangles with the same angles (taken, say clockwise), i.e. all similar to one another? This is also a two-dimensional space (because two triangles S and T are similar if and only if S = wT +z for some complex numbers w and z).
Quadrilaterals provide richer pickings. Let's start with the simplest quadrilaterals - squares. Initially let's consider squares oriented clockwise: (a,b,c,d). To be a square, the side from a to b has to have the same length as the side from b to c and be perpendicular to it. This can be expressed by the equation
b-a = i(c-b)
Also the side from b to c has the same length as the side from c to d and is perpendicular to it
c-b = i(d-c)
These two linear conditions ensure that (a,b,c,d) is a square so the set of all clockwise oriented squares is a two-dimensional subspace.
What about the set of all squares (both orientations). This is not a subspace. However it is contained within the set of all parallelograms which is a subspace. Indeed, for (a,b,c,d) to be a parallelogram it is necessary and sufficient that the midpoints of the diagonals coincide. Thus the set of all parallelograms is defined by the single equation
a + c = b + d
and therefore the space of all parallelograms is 3-dimensional ("all" implies that reflections are also allowed). This implies the rather curious fact that every parallelogram is the sum of two squares and all parallelograms arise in this way.
For rectangles the conclusions are similar: the set of all rectangles is not a subspace but if we restrict to rectangles with the same aspect ratio we get a two-dimensional subspace.
For rhombi with one interior angle fixed we also get a two-dimensional subspace (otherwise they span the full space of parallelograms).
For trapezia (a,b,c,d) with the side from a to b parallel to the side from d to c we have the equation
b-a = -k(d-c)
where k is the ratio of the parallel sides (the aspect ratio). If all aspect ratios are allowed we don't get a subspace whereas if k is fixed we get a three-dimensional subspace. For trapezia, k will be real; but there are more general classes where k is complex number representing polygons with opposite sides inclined at a fixed angle and with fixed aspect ratio.
I will consider one more class of quadrilaterals that is not so well known - indeed I don't know if they even have a name. I shall call them DOEs because they are quadrilaterals whose Diagonals are Orthogonal and Equal. Of course there are many other generalisations but DOEs are interesting because, as we shall see, they are a sort of companion to parallelograms.
Suppose that (a,b,c,d) is a quadrilateral. The necessary and sufficient condition for it to be a DOE is
c - a = -i(d - b)
This constraint is linear so the set of DOEs is a three-dimensional subspace. Notice that quadrilaterals which satisfy c-a = +i(d - b) are another family of DOE-like quadrilaterals; the subtle difference between them and the original DOE family is that the angle from ac to bd is 270 degrees rather than 90 degrees.
We now examine some of these quadrilaterals in the language we used to describe the Petr-Douglas-Neumann theorem. The 4 special quadrilaterals are
P0 = (1, 1, 1, 1), the degenerate quadrilateral
P1 = (1, i, -1, -i), an anticlockwise square
P2 = (1, -1, 1, -1), a digon described twice
P3 = (1, -i, -1, i), a clockwise square
It follows from the equations defining parallelograms and DOEs that the linear span of P0, P1, P3 is the space of parallelograms and that the linear span of P0, P1, P2 is the space of DOEs.
We also note that the operators S1, S2, S3 are associated with apex ear angles of 90, 180, and 270 degrees; so the ears are apexes of right-angled triangles on the left of an edge, midpoints of edges, or apexes of right-angled triangles on the right of an edge.
There are essentially only two different ways to apply the Petr-Douglas-Neumann theorem to a quadrilateral. We can first apply the operator S2 and then the operator S3, or we can apply S3 and then S2; in either case the result will be a square. The proof of the Petr-Douglas-Neumann theorem however also shows that the first case (applying S2 first) gives a quadrilateral in the span of P0, P1 and P3 (so a parallelogram) and the second case (applying S3 first) gives a quadrilateral in the span of P0, P1 and P2 (so a DOE).
The last two statements are actually well-known geometrical theorems (Varignon's and Von Aubel's theorems respectively). The discussion also proves that, in any parallelogram, the apexes of right-angled triangles erected on its sides form a square; and also, in any DOE, the midpoints of its sides form a square.
All of this suggests that there may be similarly interesting theorems about pentagons and other n-gons. For example, there are 4 different regular pentagons: two normal pentagons oppositely oriented, and two pentagrams. What special properties are enjoyed by pentagons which are in the linear span of two of these? So far as I know (which is not very far) the study of sums of polygons is not at all well-developed.
Saturday, 24 August 2024
A quiz about limericks and ChatGPT
There's been loads of discussion recently about how good ChatGPT is in various domains. I think it is clear that, in simple mathematics, it is no match for a human. But there are many claims that in less precise domains it can exceed human ability. So here are two limericks on the theme of apostrophes, possessives, and plurals. One is written by a human, the other by ChatGPT. I'd be grateful for any reader commenting on which is which.
There once was a writer, quite stressed,
Whose grammar was put to the test.
With plurals and "it's,"
And possessive misfits,
They found English a baffling mess.
Said Fowler in mood quite expressive,
There's one thing on which I'm obsessive,
Mistakes apostrophic,
I deem catastrophic,
The plural is not the possessive.
I know this blog has very few readers so I will let at least a month go by before reporting the comment consensus.
Monday, 15 July 2024
Problems with ChatGPT
I've been an occasional user of ChatGPT for about a year. It occasionally is truly impressive but today I had an interaction with it that, in many ways was both weirdly human and stubbornly wrong. I had been investigating a geometrical question:
What is the condition that the midpoints of a quadrilateral form a square?
I began by telling ChatGPT that I knew that the midpoints of a quadrilateral always formed a parallelogram. It agreed and gave me the proof that requires two applications of the midpoint theorem. Then came this dialogue
Me: For what type of quadrilateral is this parallelogram a square?
ChatGPT: The parallelogram formed by the midpoints of the sides of a quadrilateral is a square if and only if the original quadrilateral is a rectangle.
This was followed by several lines of proof which included the claim that the diagonals of a rectangle intersect at right angles. ChatGPT's claim is false and I pointed this out saying that it could not be true for long thin rectangles. So then....
ChatGPT: You are correct, and I apologize for the confusion. Let's revisit the conditions under which the parallelogram formed by the midpoints of a quadrilateral's sides is a square.
Then came...
ChatGPT: For the parallelogram formed by the midpoints of a quadrilateral's sides to be a square, the original quadrilateral must be an isosceles trapezoid.
More dialogue in which I again refuted this claim with long thin isosceles trapezoids to which I got:
ChatGPT: I apologize for the confusion earlier. You are right; neither rectangles nor isosceles trapezoids in general guarantee that the midpoints of their sides will form a square under all circumstances. Let's clarify the exact condition needed for the parallelogram formed by the midpoints to be a square.
ChatGPT: For the parallelogram formed by the midpoints of a quadrilateral to be a square, the quadrilateral must be a rhombus.
Another refutation by me and then ChatGPT returned to its original declaration that the quadrilateral had to be a rectangle. And finally...
ChatGPT: I appreciate your patience and the opportunity to clarify this correctly.
At that point I could not get much change in ChatGPT's replies. Its geometrical reasoning was superficially plausible in that it set out its arguments in a logical progression of steps. I have to confess I would have been hugely impressed had it got its logic correct. But the weirdly human aspect of it was its insistence, despite all the evidence, that it was right all along.
And I guess the moral of this interaction is that, despite its answers being couched in the most plausible of clothes, it was entirely wrong. And so, be careful, perhaps it is wrong lots of times.
Update 9 February 2025:
I returned to ChatGPT 6 months later and asked the same question. This time it was not only correct but actually extended my knowledge.
Friday, 12 July 2024
Napoleon's theorem
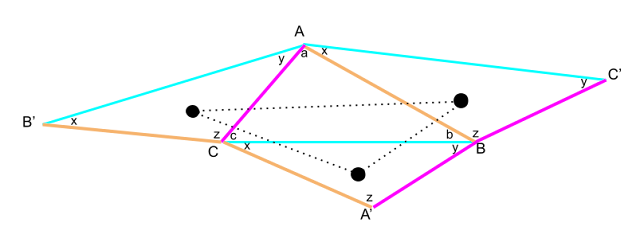
I'm an avid follower of Mathologer videos and his latest on the Petr-Douglas-Neumann theorem was well up to his high standards. I hope to write another post on that video but today I am commenting on a special case - Napoleon's theorem - that many others have also discussed.
Seemingly there is no definite connection with Napoleon Bonaparte, or any other Napoleon, but the theorem does seem to have made its debut in the mathematical literature in the early part of the nineteenth century. So, given that Napoleon had many renowned mathematical friends and was keenly interested in science, it is possible that a connection may exist.
In its basic form Napoleon's theorem is:
Let ABC be any triangle. Then the centroids of the 3 equilateral triangles with bases AB, BC, CA erected on the outside of triangle ABC form an equilateral triangle.
There are several proofs and generalisations. The proof that I give below is similar to the one here but handles one of the known generalisations of the theorem.
First some terminology.
We shall deem two triangles to be similar if one can be transformed into the other by a translation, scaling factor, and rotation. In particular this means that the set of interior angles of one triangle is the same as the other and these angles occur in the same order around their triangle. The second condition is not always part of the definition of similarity.
If we think of our similar triangles as lying in the plane where every point is a complex number then we have the following necessary and sufficient condition that the triangle with vertices (z1, z2, z3) is similar to the triangle with vertices (w1, w2, w3):
Thursday, 18 April 2024
Conway's circle theorem
In my previous post on Three Youtube videos I discussed the Mathologer video which states and gives an elegant proof of John Conway's circle theorem. In this post I want to give a more pedestrian proof that requires only simple angle chasing. Some of the video commenters appear to have found similar proofs so my contribution may simply be to present a proof accompanied by diagrams to make it easy to follow along.
For completeness I'll state the theorem. It concerns an arbitrary triangle where, in this diagram, I colour the triangle sides red, green, and blue. The triangle sides are extended by red, green, and blue lines as shown; all red segments are of the same length and, similarly the blue segments and the green segments.
Saturday, 13 April 2024
Three Youtube videos
When Youtube was launched in 2005 I didn't expect that an internet service for amateurs to share home videos would be more than a niche interest. I was totally wrong. In less than a year it was attracting 100 million views per day and in December 2006 it was acquired by Google. Nowadays Youtube is one of the first ports of call when searching the internet with videos on topics ranging from "How to fit a mirror to a bicycle" to full-length courses on Moral Philosophy.
In this post I want to discuss three videos I enjoyed today (see how my conversion is complete!) which are loosely linked in that they challenge mainstream societal ideas.
The first of these is a 10 minute presentation by Zach and Kelly Weinersmith on the feasibility of creating settlements on other worlds. I came across this video by accident (a common Youtube occurrence) because I follow Zach's clever daily cartoon "Saturday Morning Breakfast Cereal".
The Weinersmiths have just published a book "A City on Mars". Apparently they began the project with an optimism that one might summarize with "Yes, there are technical problems, but human beings are good at solving such problems. Let's look at what has to be done." However, in their video today they admitted to a complete volte-face. As a result of their research for the book they are now extremely pessimistic about whether these problems will be solved any time soon. Their conclusions are argued at greater detail in their book but this video is a punchy summary of what they found.
I'm pretty sure that scientists working on how human beings can live on Mars or the Moon are well aware of all the difficulties. However, outside that community of experts, I think people generally would presume that our aspirations to colonise other worlds are not just pie in the sky (pun intended). Who can blame them when our entertainment culture routinely serves up movies like "Don't Look Up".
So, all credit to Zach and Kelly for stepping up to fill a hole in the public understanding of science.
My second Youtube video is the latest in the excellent series of mathematics videos by the Mathologer Burkard Polster. It is very hard to make watchable mathematics videos because people's math backgrounds vary from the all too common "I've never got math. It's just not for me" through "I wish I'd paid more attention at high school and could appreciate some of the more important aspects" to "I love math but still find it hard". Polster's videos span a range within the second and third of these categories. He has an expositional style that is clear, conveys genuine enthusiasm without distracting witticisms, and uses computer animations brilliantly.
Today's video, entitled "Conway's Iris Problem", starts from an arbitrary triangle, constructs 6 additional points, and proves that these points lie on a circle. Simple hypotheses, a simple construction, and an easy to understand conclusion. What is not so simple is the reasoning towards the conclusion. We are conducted through two slick proofs supported by the usual helpful animations.
Mathematicians often use phrases like "This is a beautiful proof" which often mystifies a non-mathematician. The great challenge for a math educator is to awaken a sense of wonder in a student when understanding a clever proof. I don't know a better metaphor than "beauty" but I know it when I see it.
Anyway this demonstration is beautiful. Polster knows it and does a great job at helping viewers experience that pleasure.
Nowhere in the video (or in any of the Mathologer videos) does Polster say that what he is describing is useful or economically worthwhile. He is concerned solely with getting across the pleasure of understanding the reason a mathematical statement might be true. When I was a young student myself this was generally the spirit in which mathematics was taught. Things are different today. It has become commonplace for teachers to motivate mathematics by appealing to its utility in the real world. As a result it is widely believed in our society that mathematics is valuable because it is such an essential tool in engineering and science.
Of course we must not lose sight of this great utility of mathematics. But if that is the only reason we study it then something has very definitely been lost. For that reason I loved this video which celebrates the purity in Pure Mathematics.
The final video I'd like to discuss is by the physicist and philosopher Sabine Hossenfelder. I had seen some of her older videos and, while I admired her clarity of thought and precision of language, I had always wondered whether some of her negative comments about the scientific establishment might stem from career frustration. However her opening sentence in her latest video, in which she indicated sadly that her career as a physicist had transitioned into a Youtube poster, was so refreshingly candid that I was hooked immediately.
Hossenfelder gives an account of her education and career. She was a star student who thoroughly enjoyed her time as an undergraduate and it seemed to her that her intellectual life of a physicist would mirror the lives of physicists who had inspired her to begin with. However, despite having grades that a few years earlier would have earned her an academic position, she found it quite hard to make progress and embarked on a punishing life of going from one short-term research contract to another. For young scientists trained in the 1990s and later this is quite a common problem. This treadmill continued essentially till the pandemic arrived whereupon she changed her career and became a Youtuber.
During this time she came to realise that the model of academia was rather different to that of the great generation of physicists in the 1920s and 1930s and she bitterly summarizes her conclusions. A modern university department depends on research funding to survive. Permanent senior staff have to continually apply for research grants. These grants not only fund the planned research project but also come with an "overhead" component that pays for short-term researchers and contributes to the salaries of permanent university staff. Proposals to funding bodies have to be for projects that can be completed in a three to five year period and must not be too risky that they will frighten the funding body. A university department, if it is to flourish, must insist that its staff diligently seek out research funding - and this often influences how research proposals are formulated.
I was a lecturer and professor in four universities from 1970 to 2012 and watched this transition with increasing unease. I completely agree with Hossenfelder's analysis.
It seems that I am not the only one who thinks Hossenfelder's criticisms are valid. In the week since her video appeared it has attracted nearly thirty thousand (!) comments. I have been through some hundreds of these and have not come across any commenter who disagrees with her - in fact the vast majority of them echo her opinions with stories of their own.
This is a video which challenges the way universities (particularly science departments) operate. Hossenfelder has done an excellent job in bringing this to the attention of a large number of critics. It will not win her friends from the establishment but she can take comfort from the fact she has far more readers than even the most renowned senior researchers.
Saturday, 23 March 2024
The James Grimes card trick
I recently came across a Numberphile video posted by James Grimes which I found quite diverting. James described a numerical conjuring trick for which it was not entirely obvious why it worked. His trick (minus all the conjuring patter) goes as follows:
- The performer presents 10 playing cards with face values 1, 2, ..., 10 to the spectator and invites them to divide the cards into two arbitrary subsets A and B of 5 cards each.
- He then gets them to arrange A into an increasing sequence; and then to arrange B into a decreasing sequence. The second sequence is placed below the first.
- Then he gets them to write down the 5 differences of corresponding terms in the two sequences (here "difference" means absolute value of the difference).
- Finally he gets them to add these 5 numbers together.
Surprise, surprise: the answer is always 25.
James eventually gave the reason for this surprise. Writing the increasing and decreasing sequences as a1 a2 a3 a4 a5, and b1 b2 b3 b4 b5 it turns out that, for every pair ai bi, (whose difference is to be calculated) one of ai and bi is in the range 1 to 5, and the other is in the range 6 to 10.
To see this write L (low) for any of the values from 1 to 5 and H (high) for any of the values from 6 to 10. Suppose the first sequence has r low numbers and s=5-r high numbers so that it looks like LrHs. Then the second sequence has 5-r=s low numbers and 5-s=r high numbers so that it looks like HrLs. So each pair of positions must have an L and an H.
From this it follows that each difference has the form H-L and so their sum is the sum of the H's minus the sum of the L's. This comes to 25.
I have laboured this little argument for two reasons. The first is that I found it hard to find it myself and was embarrassed by its simplicity. The second is that, from it, one can see a much more general result.
Plainly the same type of argument will apply if one starts with the first 2n integers rather than 10. In this case it turns out that the sum of differences is n2 which is rather neat. Also it applies if one starts with any collection of 2n numbers (and I said "collection" rather than "set" because repeats would be allowed). In that case the sum of differences is always the sum of the H's minus the sum of the L's whatever that turns out to be.
Both these observations were made by James himself. But even more is true. All that matters is that the two sequences are of the form LrHs and HrLs. This is a much weaker condition than that the first sequence is increasing and the second is decreasing. Even a weaker a condition can be required: so long as matching pairs comprise both an L and an H this will be enough.
In his video James asked for variations on his original trick. Here is one that exploits the more general case.
The performer presents a set of cards face down to one spectator and a second set to another spectator. Each spectator draws a card from his set and the two cards are given to the performer who places them also face down to form the first cards of a pair of rows. This is repeated until all the cards have been drawn and placed in the rows thereby producing two rows of cards. The cards are then turned over and the corresponding differences are calculated and summed. The performer predicts the sum.
Before performing the trick the performer has arranged that one set of cards contains low (L) cards and the other high (H) cards. The spectators will not notice this because the performer places each pair of cards randomly in either the first row or the second row; therefore when the cards are turned over all evidence of lowness and highness will have disappeared.
Thursday, 7 March 2024
Monday, 19 February 2024
The Impossible Chessboard Puzzle
That is the general format of the puzzle and the two inmates have to devise a strategy whereby Joe can reveal the location to Donald.
The problem, of course, is to work out how Joe can somehow manage to tell Donald the location of the key. They know nothing in advance of the disposition of heads and tails, and no further communication between them is allowed.
- Joe computes the colour of the given board b as a t-bit binary number x
- Joe converts the position of the key as a t-bit binary number y
- Joe calculates z = x + y and flips the bit at position z of the board, giving a new board d
- Donald computes the colour of the board d. This is a t-bit binary number w that identifies the position of the key.
Thursday, 18 January 2024
My friend Nelson Stephens
My friend Nelson Stephens died peacefully, with family members at his side, on 8 January 2024. He had a wonderful sense of humour and he would have enjoyed the ambiguity in the previous sentence. That humorous side of him was evident on many occasions: as limerick writer on the blackboard in the Mathematics common room in Cardiff, in his gentle takedowns of self-important colleagues, in his ability to find absurdity in the most prosaic of situations, and in his delighted grin when he managed to lull you into an error. All benign, none malign.
I met Nelson in 1972 when he joined the department of Computing Mathematics at University College, Cardiff. I warmed to him immediately and for 10 years we were close friends, played badminton and Othello together, enjoyed our families meeting for dinner, and we went on many outings together. I particularly remember the occasion when Fred Lunnon led a walk to the Waterfall Country around Ystradfellte in the Neath Valley. We had to make a number of tricky river-crossings that Nelson struggled cheerfully with (he had a life-long foot problem that must have affected his balance).
The department specialised in using computers to solve problems in Pure Mathematics. This was Nelson's forte and he had already done significant work both in his PhD studies and at the Atlas Computing Laboratory in Number Theory where he was an expert in elliptic curves. This esoteric subject eventually became very important in cryptography and Nelson remained an active researcher in the field throughout his academic career. Luckily for me his expertise and interests were much wider than that and I knew I was fortunate to have a colleague that I could discuss mathematics with.
In 1975 I attended a series of lectures he gave to our Masters students, largely working through some of the chapters of Hopcroft and Ullman's new book which became very influential in the young field of data structures and algorithms. I learnt a great deal from these lectures and particularly enjoyed the lectures on the Finite Fourier Transform and Matrix Multiplication. Nelson and I began to think about the general context for these two topics: the computation of several bilinear forms. This this led to our publishing two papers that are still being cited. I remember how this research was kick-started. Nelson met me in the department one morning excited by an idea he'd had in bed: it involved solving a generalised eigenvalue equation and we both knew it was a breakthrough.
I left Cardiff in 1982 but we remained very close friends with me visiting him several times over the years. Whenever we met we slipped back into an easy familiarity sharing our personal pleasures and problems. On one of my visits he took me to his bridge club in Cardiff. I was nothing like as good a player as him but that evening we had a very good game together topping the field and winning about £40.
We never published together again although there was one year when I managed to interest him in an algebraic problem. In a very short time he produced a computer program that generated a large amount of useful data that we pored over together making various conjectures. Nelson then applied for and received a small grant from the UK Engineering and Physical Science Research Council to enable us to visit one another. Unfortunately this never came to fruition because I emigrated to New Zealand.
Nelson left Cardiff after about 20 years to become Professor of Computing at Goldsmiths College, London. He did not give up his home in Cardiff and undertook the challenging London-Cardiff commute. On the only occasion I visited him at Goldsmiths I had the impression that he was coping with the new challenges there but it was very hard work.
Throughout his life Nelson took a keen interest in politics. He was a staunch member of the Labour party and I can attribute my own passage from the political centre to the political left partly to him. I remember once joking with him that the Labour party was his natural home as he shared his birthday with Tony Blair.
One of the things I particularly admired in him was his personal modesty. We both deplored that new breed of academic who have unbounded egos. Nelson was not like that. He spoke frankly when it was warranted but never rudely. He listened attentively rather than switching off and using the time you were speaking to prepare his next statement about himself. As a result conversation with him was a delight.
Farewell, my good friend. You leave me with a treasure trove of wonderful memories.








.jpg)


